Navigation auf uzh.ch
Navigation auf uzh.ch
23 August 2016
The article “The Price of Complexity in Financial Networks”, written by Stefano Battiston, Guido Caldarelli, Robert M. May, Tarik Roukny, and Joseph E. Stiglitz, published on PNAS on Tuesday, August 23, 2016 (available here) develops a mathematical model to compute the default probability of banks in a network of credit contracts. One of the main contributions of the work is to provide an explanation why the complexity of the network of financial contracts decreases the ability of regulators and financial institutions to assess and mitigate systemic risk. While there certainly is some intuition among practitioners for this undesirable aspect of financial complexity this is the first work that explains mathematically how this effect emerges from the interdependence of the balance sheets.
The mechanism responsible for this effect is the following. For example, a small uncertainty over the recovery rate (i.e. the percentage of money recovered from a contract’s value when a counterparty defaults) on individual contracts gets compounded multiplicatively along chains of connected banks. The same applies for the uncertainty over other contract characteristics such as leverage, or expected return. As a result, the more complex the network of contracts is (i.e. the more numerous and longer the chains of contracts are), the larger is the uncertainty on the estimation of the probability of a systemic default that both regulators and market participants can make.
More in general, we study the uncertainty on the estimation of systemic risk that a regulator could make by knowing the whole set of contracts, with some small limitations. It turns out that the small errors on most of the relevant parameters can easily lead to large errors on the probability of systemic default.
To understand more precisely how this comes about, the paper provides an analytical example with three simple network architectures: a star, a chain and a ring (see Figures A and B below). The probability of systemic default can be computed in closed form, as well as its sensitivity to the main parameters. The network structure affects the exponent of the leading term.
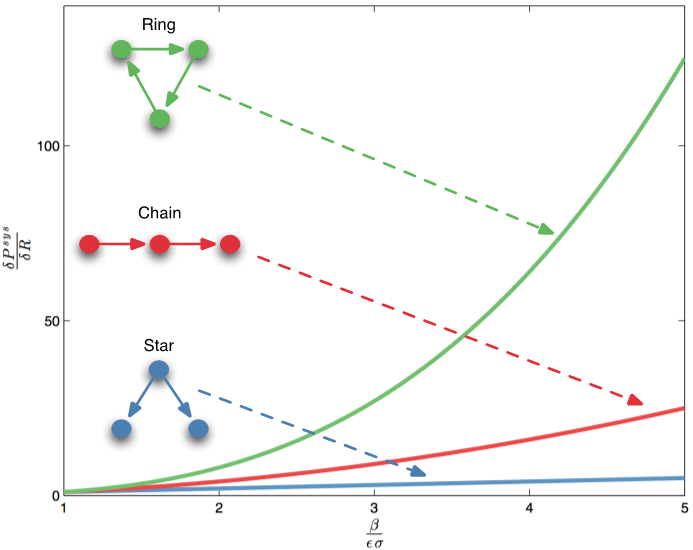
Figure A. The sensitivity of the probability of systemic default is amplified by the network structure. Curves represent the leading term of the sensitivity as a function of the ratio between the interbank leverage and the maximal loss on the external assets.
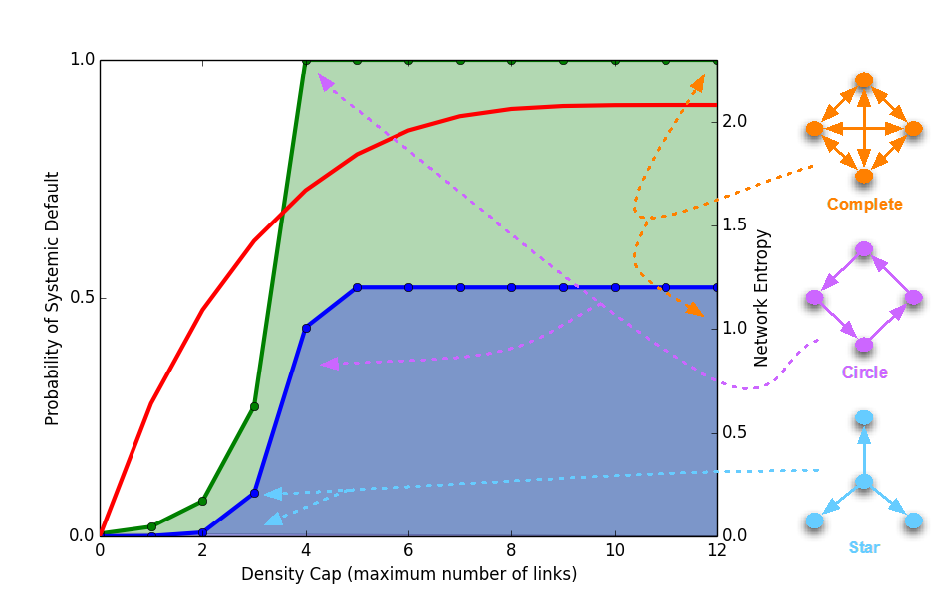
Figure B. The probability of systemic default as a function of the maximal network density. We consider all feasible network configurations for a given cap on link density: The green and blue areas represent the range of possible values of probability of systemic default for two parameter sets (see more details in the paper).
The article contributes to several on-going debates among academics and practitioners including:
The work was carried out at the FINEXUS Center for Financial Networks and Sustainability (www.finexus.uzh.ch) of the Department of Banking and Finance, at the University of Zurich, in collaboration with several international partners: Free University of Brussels, IMT Lucca, Oxford University, and Columbia University.
The work is part of a broader research agenda of FINEXUS on financial networks and systemic risk funded by the Swiss National Fund and by several European projects (www.dolfinsproject.eu; www.simpolproject.eu). Recent related research includes:
More details on “The Price of Complexity in Financial Networks”
By complexity of the network structure we mean here for example that a ring network is more complex than a chain network or a star network because it contains more or longer paths among nodes. Figure C below illustrates two simple cases of network architectures with three banks: a star and a ring. By interconnectedness we mean here the number of pairs of market players engaging in a contract out of all the possible pairs.
One the one hand, complexity is assumed to increase the ability of financial institutions to hedge risks more effectively and to offer better services to the real economy. On the other hand, complexity is also regarded as a source of information asymmetries and collective moral hazard. Indeed, if the probability of a systemic default and its social cost becomes very uncertain, then it is more likely that risk-averse regulators would concede to banks’ requests of rescuing the financial system with public funds in case of downturn. Because financial institutions anticipate being rescued, they tend to take more risk than they would otherwise.
The financial crisis of 2008 and the inadequacies emerged in its aftermath has lead to the revision of the global regulatory framework for banking institutions under the so-called Basel III Accords. In particular, capital requirements for banks are intended to make individual banks able to withstand infrequent but large losses on their assets. The calibration of such requirements is conducted both based on historical data (e.g. aiming at the 99th percentile of the loss distribution) and based on specific stress-tests.
What regulators have come to realise is that estimations of capital requirements do not take enough into account, if at all, the potential losses coming from the interdependencies in the financial system. Indeed, institutions are connected in networks in several ways both directly, via contracts among each other (loans, bonds, repurchasing agreement, derivatives, etc.), and indirectly, via exposures to common assets. The default probability of one institution, and hence the value of its debt, depends therefore on the default probability of all of the other institutions in the network
It is of course in the nature of financial contracts among banks that there is a risk that a borrower does not honour its obligation, be it a firm, a household or another bank. Even if the lender may have the right to seize the assets of a defaulting bank or if some collateral was posted as a guarantee, usually there are some bankruptcy costs that imply that counterparties would recover much less than what was agreed in the contract (i.e. the so-called recovery rate is less than one). The recovery rate for the counterparties depends on various factors including the value of the collateral (if any), the liquidity of the market for the banks’ assets that have been liquidated, the loss of social or organizational capital of the defaulting bank, and legal costs to settle the bankruptcy process.
While the interest rate on a loan is meant to compensate investors for their risk, the problem is that losses tend to be unexpectedly larger precisely when a financial crisis is looming. For instance, if banks hold large amounts of overvalued assets, as it was the case for mortgage-backed securities in the crisis of 2008, then the counterparties of a defaulting bank would not be able to recover much of the initial value of a contract by liquidating those assets.
If there were no unexpected bankruptcy costs, i.e., if there were no losses in the process of recovering collateral and liquidated assets from one’s counterparties, or if everyone could anticipate the losses exactly, then the complexity of the financial network would not matter.
In reality, however, there are often unanticipated losses. And in a mark-to-market environment, the deterioration of the financial situation of a bank implies a loss on the balance-sheets of its counterparties (because of the devaluation of the contracts that they have established with the bank). But then, in turn, the counterparties of those counterparties would also need to record a loss. It is of course in the interest of banks to avoid or delay the recognition of these losses on their balance sheet, in the hope to compensate them with future profits. But in a downturn they are eventually forced to do a sudden and painful revaluation of their assets. As a result, mark-to-market is a double-edged sword. It is good because it avoids future sudden devaluation, but it is also procyclical, i.e., prone to creating downward spirals through the network of contracts.
On the one hand, the ability of a bank to make contracts with any other bank in the system increases its ability to diversify the risk. On the other hand, the resulting complexity comes with the price that “everybody knows less.” Indeed, either a higher complexity of the individual contracts or a higher complexity of the structure of contracts implies that market participants and regulators know less precisely the probability of individual and systemic default. Although there are individual incentives to be part of a complex financial network, our article shows quantitatively the existence of so-called “negative externalities,” which eventually translate into potential social costs.
More generally, our results show that higher interdependence on the credit market among banks decreases our ability to make estimates on default probabilities and hence to correctly price debt instruments. One possible approach to this problem could be to increase the complexity of the regulation in order to match the complexity of the financial market. However, in this article we show that there are intrinsic limitations in the accuracy of estimating the probability of default, which implies that increasing the complexity of regulation may not be an appropriate way to address market complexity. Hence, a potential tradeoff emerges between financial stability and market complexity.
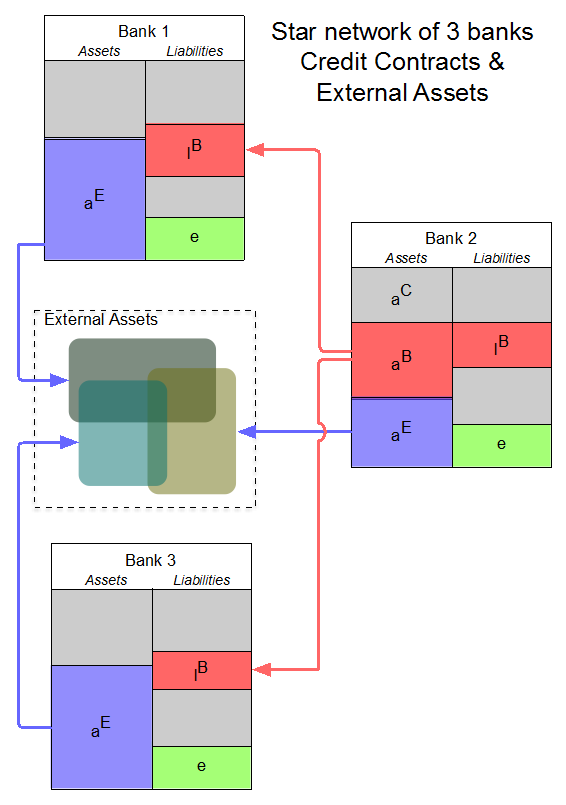
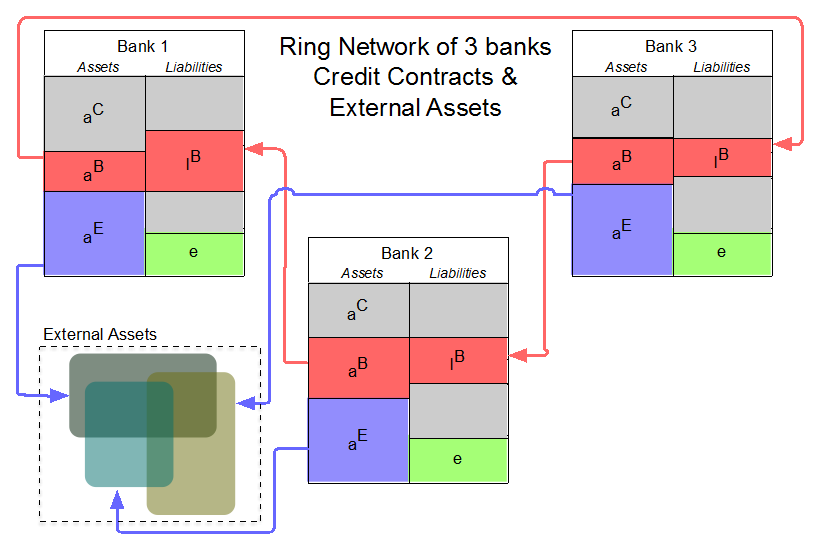
Figure C. (Left) Example of a star network architecture. Bank 2 lends to both banks 1 and 3. All banks invest in correlated external assets. (Right) Example of a ring network architecture. Bank 1 lends to bank 3 which in turn lends to bank 2 (a configuration often occurring in real-world interbank credit markets). All banks invest in correlated external assets.