Default Ambiguity: Credit Default Swaps Create New Systemic Risks in Financial Networks

By Steffen Schuldenzucker, Sven Seuken, and Stefano Battiston (University of Zurich)

In a network of simple financial contracts, the problem of “who pays what to whom” is not trivial but solvable, following well-established approaches. However, as we reveal in this new paper, just published in Management Science, the introduction of derivative contracts in the network may make it impossible to determine even which institutions should be considered in default during a crisis. How can we manage this new source of systemic risk?

More in detail, we extend the simultaneous clearing model in the tradition of Eisenberg and Noe (2001) to credit default swaps (CDSs), i.e., financial derivatives that depend on the default of another reference entity. If the reference entity is itself a financial institution, the simultaneous clearing problem may have no solution, or multiple conflicting solutions, a phenomenon which we call default ambiguity. This remains true even when regulatory authorities have perfect information about the network structure. We develop a new graph-based analysis framework for this scenario. We use it to derive sufficient conditions under which default ambiguity is eliminated and to discuss the effect of regulatory policy on default ambiguity.

Read the paper: “Default Ambiguity: Credit Default Swaps Create New Systemic Risks in Financial Networks.” Steffen Schuldenzucker, Sven Seuken, and Stefano Battiston. Management Science. Published online: 26 June 2019. (PDF, open access).

Follow us: Stefano Battiston on Twitter (@zbattiz), Facebook.

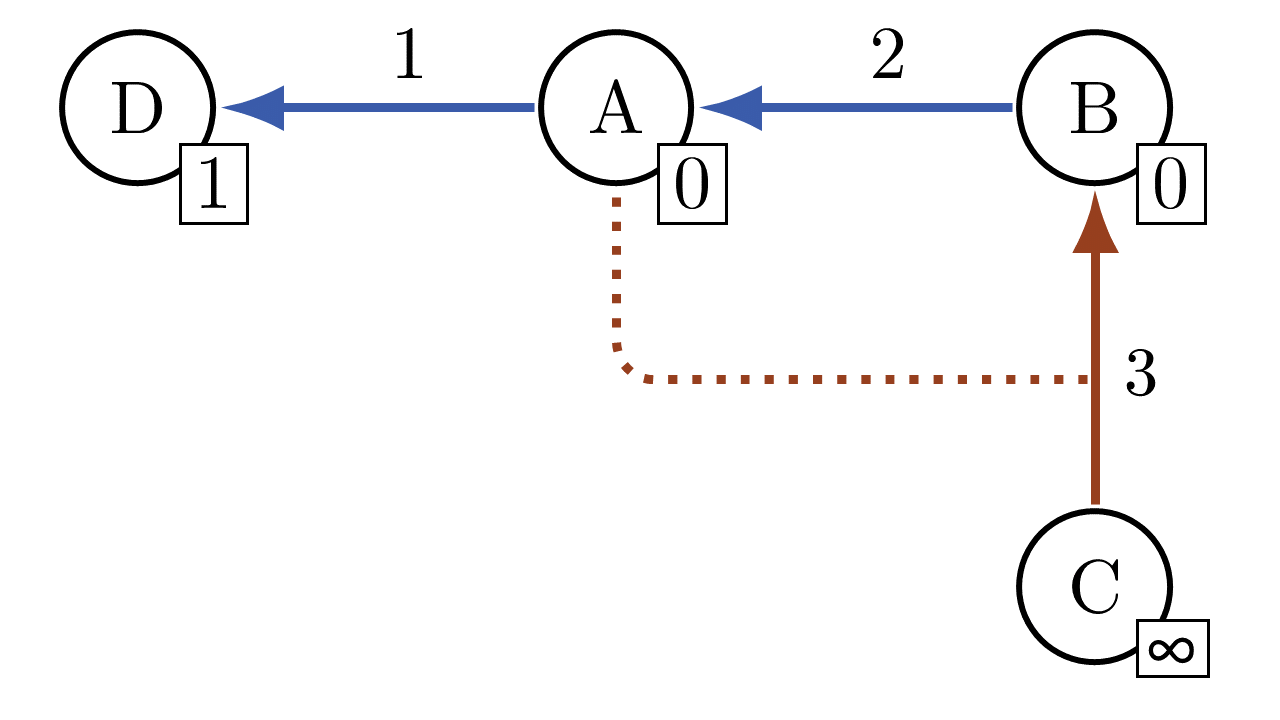
Example: The figure (click here for an animated version (GIF, 309 KB)) depicts a simple example for default ambiguity. For simplicity, assume that defaulting banks do not pay any of their obligations (i.e., there is an exogenous default cost of 100%; in the paper, arbitrary levels of default costs are considered). Institution B owes an amount of 2 in debt to A and A owes 1 to D (blue arrows). B holds a CDS where C makes a payment of 3 in case A defaults (orange arrow and dashed line). In addition to their interbank assets, D has external assets of 1 and C has infinite (sufficiently high) external assets and can thus always fulfil its obligation in the CDS. The default of A is ambiguous because it would imply a payment from C to B and thus back to A, which implies solvency of A, and vice versa. At a higher level, this ambiguity occurs because A indirectly holds a CDS on itself via B.

Methods: We model financial networks based on the debt clearing models by Eisenberg and Noe (2001) and Rogers and Veraart (2013). We define an extension to credit default swaps. Following said prior work, we assume a static model where a financial system is given exogenously, and all contracts are evaluated simultaneously. That is, we are looking for a collection of recovery rates that simultaneously satisfy the basic principles of bankruptcy law: banks with sufficient assets to meet their liabilities must do so and defaulting banks must pay out all their assets to creditors in proportion to the respective liability. Banks may further incur default costs and lose a percentage of their assets upon defaulting. The clearing problem is non-trivial because payments can depend on each other in a cyclic manner. We introduce a new analysis framework, the colored dependency graph, to study these dependencies.

Results: We show that in financial networks with CDSs, the clearing problem may have no solution and even when it does, there may not be a solution that maximizes the equity of each bank simultaneously (in a Pareto sense). The latter case is problematic because a clearing authority would have to make a choice among solutions, which would imply favoring the equity (and thus shareholders’ profits) of one bank over that of another one and this may lead to major lobbying activities. Non-maximality hinges upon the presence of naked CDSs, i.e., CDSs that are held without also holding a corresponding debt contract. These CDSs are often viewed as speculation on default of the reference entity. Non-existence arises only if such CDSs appear in a cycle, in a way made precise by our colored dependency graph.

Insights for Discussion: At a high level, we show that default ambiguity appears due to fundamental risk and not due to counterparty risk in CDSs (see D’Errico et al. (2018)). This is why policies aimed at reducing counterparty risk, like central counterparty clearing, are not effective to protect against default ambiguity. More in detail, default ambiguity arises because the holder of a (naked) CDS may profit from the financial distress of another market participant. This property is shared by any forms of naked short selling and many other financial derivatives, such as put options. This suggests that there is a risk of default ambiguity in these markets, too. Our results further imply that, to understand the behavior of financial systems with CDSs, it is essential to consider the ternary relations they introduce, including the reference entities. We hope that the availability of transaction-level data under the EMIR reforms will enable empirical studies of these structures in the future.

Keywords: Financial Networks, Credit Default Swaps, Systemic Risk, Clearing Systems

Funding: All authors gratefully acknowledge financial support from the European Union’s FP7 and Horizon 2020 research and innovation programme [Future and Emerging Technologies Grant Agreements 610704 (SIMPOL) and 640772 (DOLFINS)]. Additionally, S. Battiston acknowledges funding from the Swiss National Fund Professorship [Grant PP00P1-144689] and from the Institute of New Economic Thinking through the Task Force in Macroeconomic Efficiency and Stability.

References (for a full list, see the paper):

D’Errico, Marco, Stefano Battiston, Tuomas Peltonen, and Martin Scheicher. 2018. “How does risk flow in the credit default swap market?” Journal of Financial Stability, 35: 53–74.

Eisenberg, Larry, and Thomas H Noe. 2001. “Systemic risk in financial systems.” Management Science, 47(2): 236–249.

Rogers, LCG, and Luitgard AM Veraart. 2013. “Failure and rescue in an interbank network.” Management Science, 59(4): 882–898.